Q1. Let M be the following matrix:

(a) Find the inverse of M.
To find the inverse of M, we need to find det(A).
det(A) = ad - bc
where

det(A) = ad - bc = (2*1) - (-3)(-2) = (2)-(6) = -4
Then, rearrange M

Multiply by 1/det(A)

This gives M^-1 of:
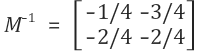
(b) Using your answer to (a) or otherwise, find the solution to the following system of equations:

2 ways of solving this question.
1) Using M^-1

2) Using Row Reduction / Subtraction

(c) Find the eigenvalues of M and their corresponding eigenvectors.
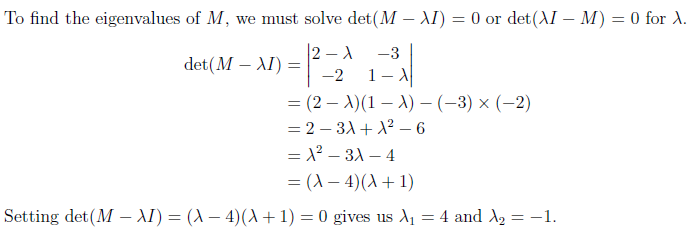



(d) Write down matrices D and P such that D is a diagonal matrix and M = PDP^-1

Important:
For the eigenvalue in first column D should match the eigenvector in the first column of P
i.e. If lambda1 is in the first column of D, the eigenvector of the corresponding lambda should come in the first column of P.